A Comprehensive Guide to Pytest Approx for Accurate Numeric Testing

Posted on 2023-09-11 Edited on 2024-05-09 In Advanced Word count in article: 3.4k Reading time ≈ 12 mins.

As a Python developer striving for accurate and efficient testing, you will likely encounter scenarios where verifying floating-point values or approximate comparisons presents challenges.

In many real-world applications, especially with scientific computing, simulations, high-performance computing, financial calculations, and data analysis, you’ll often deal with floating-point numbers.

These numbers are represented in computers using a finite number of binary digits, which can lead to rounding errors and precision limitations.

So what do you and how do you test these floating-point values?

Precision matters, but so does practicality. This is where the pytest approx module comes into play.

Just as software testing is vital for ensuring your code functions as intended, handling numerical approximations is crucial for maintaining robust test suites.

In this article, we’ll discuss how to solve floating point precision asserts using pytest approx, its purpose and functionality.

We’ll start with discussing the importance of precision in approximate testing and where pytest approx fit it.

Then we’ll discuss the syntax of pytest approx using example code and move on to implementing pytest approx onto more complex data structures.

This article will empower you with the knowledge to make informed decisions about incorporating floating point precision testing using pytest approx into your testing toolkit, ultimately enhancing the reliability of your Python projects.

Let’s get started, shall we?

Link To Example Code

Importance of Approximations in Testing

Let’s consider a financial application responsible for calculating interest rates on loans. The precision of these calculations directly impacts the financial decisions of both institutions and individuals.

Imagine a scenario where the application reports slightly inaccurate interest rates for specific loan terms because it couldn’t handle floating-point approximations effectively.

These minute discrepancies might seem trivial on the surface, but they can accumulate over time, potentially leading to significant financial differences for borrowers and lenders alike.

As you can see in this context, the importance of approximations in testing becomes evident.

Without a robust mechanism to account for slight variations in floating-point calculations, the testing process could fail to pinpoint these subtle inaccuracies.

As a result, test cases might pass when they shouldn’t, giving a false sense of security that the application is functioning correctly.

You need to acknowledge the critical role of approximations in testing and implement solutions using tools like the pytest approx module to strike a balance between precision and practicality.

The Issue With Floating Point Arithmetic

Floating-point numbers are encoded in computer hardware using base 2 (binary) fractions.

You know that the decimal fraction 0.125 can be written as 1/10 + 2/100 + 5/1000. Similarly, the binary fraction 0.001 corresponds to 0/2 + 0/4 + 1/8.

Do you notice a difference in both the above representations?

Well, the key distinction lies in the representation: the first employs base 10 fractional notation, while the second employs base 2 i.e. the denominator is a multiple of 2.

Majority of decimal fractions cannot be precisely represented as binary fractions.

Consequently, the decimal floating-point numbers you input are inherently approximated by the binary floating-point numbers stored within the machine.

This issue is easier to grasp when considered in base 10.

Take the example of the fraction 1/3. It can be approximated in base 10 as follows: 0.3, or 0.33 or even better 0.333 and so on.

Irrespective of the number of digits you employ, the outcome will never be an exact match for 1/3; instead, it will perpetually improve as a closer approximation of 1/3.

Just remember, even though the printed result may look somewhat similar to 1/3, the actual stored value is the nearest representable binary fraction.

Solve Numeric Approximation Problems Using Pytest Approx

Minor discrepancies can arise due to the inherent nature of floating-point representation, though small, can lead to failed test cases or false positives.

Pytest Approx offers a solution by allowing developers to assert approximate equality, meaning that values are considered equal as long as they are within a specified tolerance of each other.

This approach acknowledges the practical need for slight variations in calculations while ensuring that tests remain effective and reliable.

Rather than unpacking floating-point numbers during calculation or approximate comparison, you can go for a neater and more effective method using pytest approx.

Objectives

By the end of this tutorial, you should be able to:

Understand the importance of approximations in testing and the potential challenges they pose.
Understand how Pytest Approx can help accommodate acceptable differences in calculations.
Familiarize yourself with the syntax of Pytest Approx.
Implement approximation techniques for lists, arrays, dictionaries, and nested data structures.
Compare Pytest Approx with other approximation modules like Numpy’s assert_allclose.

Prerequisites

The project has the following structure:

pytest-approx-repo

To get started, clone the repo here, or you can create your own repo by creating a folder and running git init to initialise it.

Set-up and Installations

In this project, we’ll be using Python 3.11.4 and Pytest.

Install the packages by navigating to the root of the repo and running pip install -r requirements.txt.

If you’d like to use the Pytest - VS Code integration, we have a full step-by-step guide on setting up Pytest with VS Code.

Understanding Tolerance Levels

Understanding tolerance levels is crucial when dealing with numerical approximations in testing.

Tolerance determines the acceptable deviation between two numbers for them to be considered practically equal.

Imagine you’re a chef following a recipe to bake a cake. The recipe calls for 1 cup of flour and 2/3 cup of sugar.

However, due to variations in measuring techniques and ingredient densities, your cup of flour might not be the exact same size as the author’s cup, and the amount of sugar might not be perfectly aligned with the intended measurement.

In this baking scenario, the concept of tolerance becomes relevant. A small variation in the amount of flour or sugar might not drastically affect the final cake’s taste or texture.

As long as the measurements are close enough, the cake is likely to turn out delicious.

Applying this idea to software testing, tolerance levels allow us to consider two numbers as “close enough” to be treated as equal, accommodating minor discrepancies that don’t impact the overall functionality of the code.

Basic Use of Pytest Approx

Now we will implement the functionality of pytest approx. Let’s discuss the syntax and semantic of this function before we jump into it’s more complex implementations.

Syntax of Pytest Approx

The syntax for using the pytest approx functionality in Pytest is quite straightforward. You can use it to perform approximate comparisons between numerical values, accounting for the inherent imprecision of floating-point calculations.

Here’s the basic syntax:

1	assert actual_value == pytest.approx(expected_value, rel=None, abs=None, nan_ok=False)

actual_value: The computed value that you want to test.
expected_value: The expected value that the actual_value should be approximately equal to.
rel: (Optional) Relative tolerance as a float. Specifies the relative tolerance level for the comparison. Default: None
abs: (Optional) Absolute tolerance as a float. Specifies the absolute tolerance level for the comparison. Default: None
nan_ok: (Optional) Boolean value. Specifies whether to consider NaN values as equal. Default: False

The pytest.approx function will perform the comparison and determine whether the actual_value is within the specified tolerances of the expected_value.

Full documentation can be found here.

Example Code To Test Pytest Approx

Here’s a simple example to implement pytest approx:
tests/unit/test_pytest_approx_1.py

import pytest

def divide(a, b):
    return a / b

def test_exact_comparison():
    result = divide(1, 3)
    assert result == 0.3333333333333333  # Exact value

def test_approximate_comparison():
    result = divide(1, 3)
    assert result == pytest.approx(0.3333333333333333)  # Approximate value

@pytest.mark.xfail(reason="This test is currently expected to fail")
def test_approximation_failure():
    result = divide(1, 3)
    assert result == pytest.approx(0.333)  # This test will fail due to approximation

test_exact_comparison: Comparing the result of the divide(1, 3) function call, which computes 1 / 3, with the exact value 0.3333333333333333. Since the comparison is exact, the test passes.
test_approximate_comparison: This test also compares the result of divide(1, 3) with the value 0.3333333333333333, but this time using pytest.approx. This test passes because pytest.approx considers the small variations due to floating-point imprecision.
test_approximation_failure: Here we compare the result of divide(1, 3) with the value 0.333 using pytest.approx.

This test is marked as expected to fail (@pytest.mark.xfail) because the approximation tolerance (0.01 by default) is too strict, and the floating-point imprecision exceeds this tolerance.

Therefore, this test fails as expected.

pytest-approx

If you’re not familiar with the @pytest.mark.xfail decorator, it’s used to mark a test as expected to fail. Our extensive article on Pytest xFail covers this in detail.

Assert Floating-Point Numbers Are Equal - The Issue

Imagine having to do multiple floating-point number comparison using the traditional method, like this:

1	assert abs(result - expected_result) < 1e-6

It’s not only tedious but also prone to errors.

Now, imagine using the more flexible pytest approx approach:

1	assert result == pytest.approx(expected_result, abs=1e-6, rel=1e-9)

Feels more elgant and Pythony. Doesn’t it?

The lack of a universally applicable tolerance value makes it problematic, as varying scenarios might necessitate different tolerances to account for precision variations.

Absolute comparisons struggle to address the inherent imprecision of floating-point arithmetic consistently.

Recognizing this, Pytest offers a more flexible and recommended solution through the pytest.approx module.

Its approach is better suited to handling the challenges posed by floating-point comparisons, promoting accuracy and reducing the likelihood of false negatives or positives in test outcomes.

Different Approaches to Approximation

Different approaches to approximation are needed to provide a flexible and adaptable way of comparing floating-point values in various testing scenarios.

Absolute Tolerance:

Developers can set an absolute tolerance level to accept results within a certain range, ignoring minor differences.

If you want to use absolute tolerance, specify a fixed range within which the actual value can deviate from the expected value.

If the absolute difference between the actual and expected values is within this range, the comparison is considered successful.

tests/unit/test_pytest_approx_2.py

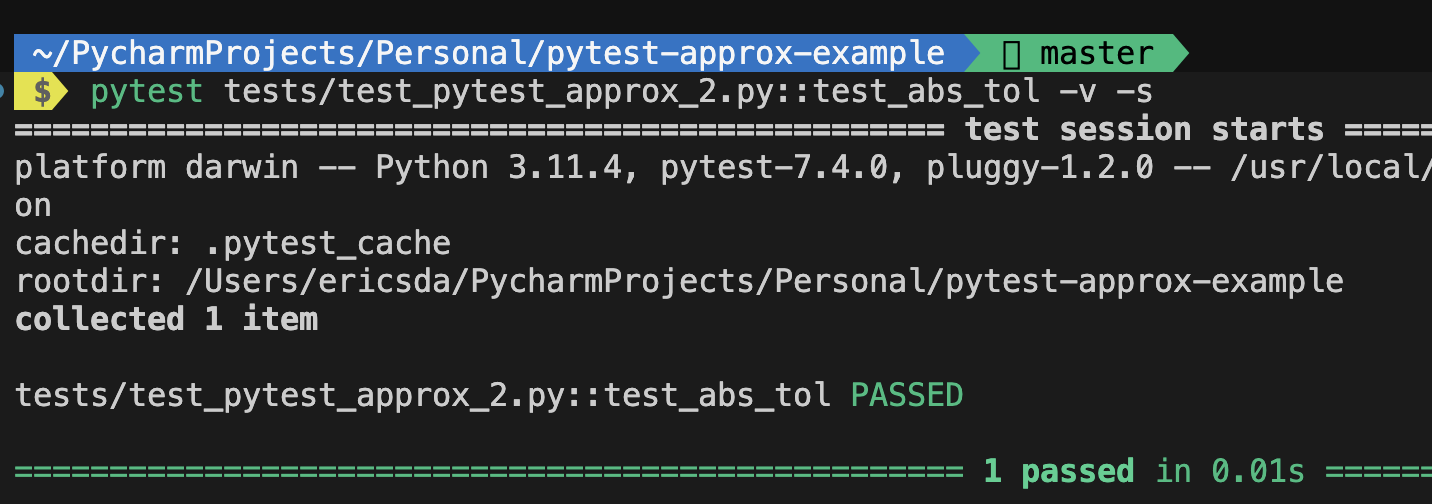
def test_abs_tol():
    # Test case 3: Using absolute tolerance
    actual_value_3 = 15.0
    expected_value_3 = 15.5
    assert actual_value_3 == pytest.approx(expected_value_3, abs=0.6)

For example, in the above code, a maximum absolute difference of 0.6 is allowed between actual_value_3 and expected_value_3. So if the difference is less than or equal to 0.6, the assertion will pass. In this case, the absolute difference is 0.5, which is less than 0.6, so the assertion passes.

pytest-approx-absolute-tolerance

Relative Tolerance:

Relative tolerance allows for variations relative to the magnitude of the values being compared. Instead of specifying an absolute fixed difference, you specify a percentage (or fraction) of the expected value as the tolerance.

tests/unit/test_pytest_approx_2.py

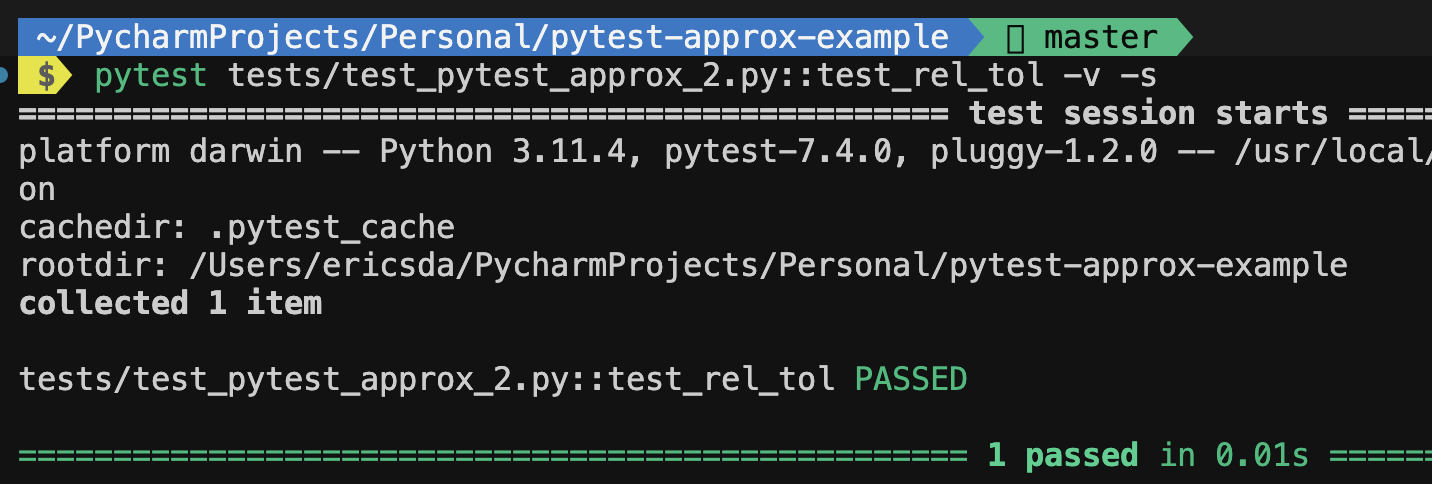
def test_rel_tol():
    # Test case 2: Using relative tolerance
    actual_value_2 = 200.0
    expected_value_2 = 205.0
    assert actual_value_2 == pytest.approx(expected_value_2, rel=0.2)

For example, in the code snippet written above, the relative tolerance is 20% (0.2) of the expected_value_2. If the relative difference between actual_value_2 and expected_value_2 is less than or equal to 20%, the assertion will pass.

This approach is useful for testing large and small values together.

pytest-approx-relative-tolerance

Scaling Factors:

Pytest Approx supports applying scaling factors to adjust tolerances dynamically based on the input data.

Scaling factors are applied to both relative and absolute tolerances, ensuring more accurate comparisons in different scenarios.

tests/unit/test_pytest_approx_2.py

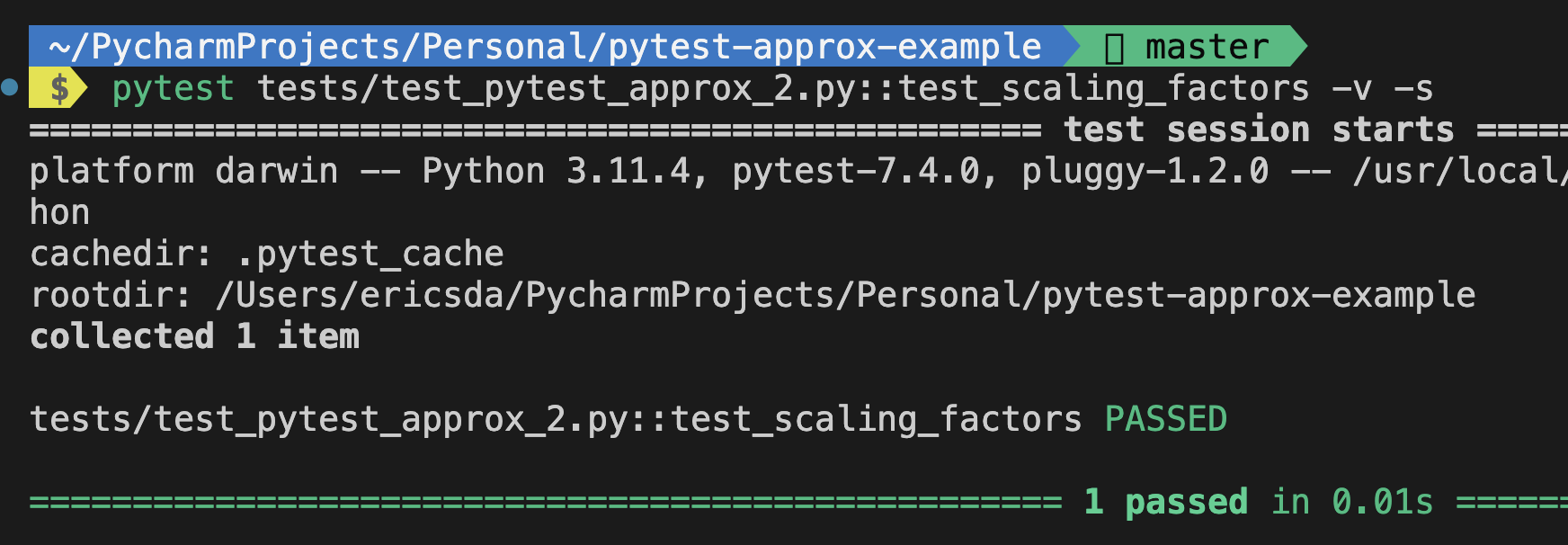
# Define a custom function that performs a scaling operation
def scale_value(value, factor):
    return value * factor

def test_scaling_factors():
    # Test case 6: Using a scaling factor
    original_value = 5.0
    scaling_factor = 2.0
    scaled_value = scale_value(original_value, scaling_factor)

    assert scaled_value == pytest.approx(original_value, rel=scaling_factor - 1)

The scale_value function takes two arguments: value and factor.

It returns the product of value and factor. This function is used to scale a given value by a certain factor.

In this case, since scaling_factor is 2.0, the relative tolerance is 2.0 - 1 = 1.0. This means the test will pass if scaled_value is within 100% of original_value, which is always true when you scale a value by a factor of 2.0.

pytest-approx-scaling-factors

Handling NaN values:

According to Wikipedia,

In computing, NaN (/næn/), standing for Not a Number, is a particular value of a numeric data type (often a floating-point number) which is undefined or unrepresentable, such as the result of zero divided by zero.

Pytest Approx allows you to specify whether to consider NaN values as equal or not.

tests/unit/test_pytest_approx_2.py

def test_NaN_val():
    # Test case 4: Handling NaN values
    nan_value = float("nan")
    assert nan_value == pytest.approx(nan_value, nan_ok=True)

The above code checks if the handling of NaN values works as expected.

pytest-approx-nan

Using Custom Comparators:

A custom comparator lets you define your own rules for comparing values within the approx function. This is particularly useful when the default tolerance doesn’t fit your testing scenario.

Developers can define custom comparators for specific data types or classes, allowing fine-grained control over the approximation process.

This approach offers flexibility in managing complex data structures or unique situations where standard tolerance levels may not suffice.

For instance, if you expect a floating-point result of 0.1 but the actual result is 0.1000001, you might still want to consider these values as equal. However, this default tolerance might not be appropriate for all cases and this is where custom comparators come into play.

All the test cases mentioned in this article use the concept of custom comparators. The test cases created to compare the expected value with original value is the working principle behind custom comparator.

Handling Complex Data Structures With Pytest Approx

Pytest Approx provides a robust solution for accurate testing.

Whether it’s lists, arrays, dictionaries, or nested data, Pytest Approx ensures that the intricacies of floating-point approximations don’t compromise your testing.

Approximating Lists And Arrays

When comparing a list of calculated values with expected results, Pytest Approx simplifies the process, allowing you to assert approximate equality without manually addressing each element’s precision.

Similarly, when you are comparing arrays you can employ pytest.approx to verify their equality within specified tolerances.

Let’s look at an example of how array calculation is handled precisely using pytest approx:
tests/unit/test_pytest_approx_3.py

import pytest
import numpy as np

# Function to calculate the element-wise square of a list or array
def calculate_square_elements(data):
    return [x**2 for x in data]

def test_list_comparison():
    expected_result = [1, 4, 9, 16]
    input_data = [1, 2, 3, 4]
    calculated_result = calculate_square_elements(input_data)

    assert calculated_result == pytest.approx(expected_result)

def test_numpy_array_comparison():
    expected_result = np.array([0.1, 0.2, 0.3])
    input_data = np.array([0.31622776601683794, 0.4472135954999579, 0.5477225575051661])
    calculated_result = calculate_square_elements(input_data)

    assert calculated_result == pytest.approx(expected_result, abs=1e-6)

Both tests demonstrate how pytest.approx can be used to handle numerical comparisons, even when dealing with arrays or lists that might have slight variations due to floating-point precision.

pytest-approx

This approach ensures accurate testing without being overly strict in requiring exact matches.

Approximating Dictionaries

For dictionaries, Pytest Approx handles key-value pairs with precision.
tests/unit/test_pytest_approx_6.py

import pytest

def test_measurements():
    expected = {
        'length': 10.0,
        'temperature': 25.5,
        'pressure': 1013.25,
    }
    
    calculated = {
        'length': 10.0001,        # Slightly different due to calculations
        'temperature': 25.4999,   # Slightly different due to calculations
        'pressure': 1013.24,      # Slightly different due to calculations
    }
    
    tolerance = {
        'length': 0.01,           # Tolerance for length values
        'temperature': 0.05,      # Tolerance for temperature values
        'pressure': 0.1,          # Tolerance for pressure values
    }
    
    for key in expected:
        assert calculated[key] == pytest.approx(expected[key], abs=tolerance[key])

In scenarios where you’re comparing calculated dictionary values with expected outcomes, Pytest Approx lets you assert approximate equality while accounting for floating-point discrepancies.

pytest-approx

Pytest Approx vs. Numpy’s `assert_approx_equal`

The approx function in Pytest is used within assertions to check if values are approximately equal.

On the other hand, Numpy’s assert_approx_equal method is used to explicitly assert the equality between two values using pytest.approx.

If you work extensively with NumPy arrays and functions or want more fine-grained control over the assertion, you can use NumPy’s assert_approx_equal.

It allows you to specify parameters like the value you want to test, the expected value, and the significant, which determines how many significant digits should match.

The distinction lies in how the tests are expressed. The pytest appprox module is more succinct and follows the pattern of other Pytest assertions, while the other method provides a more direct way to assert the approximation.

Let’s look at an example to better understand the difference:
tests/unit/test_pytest_approx_4.py

import pytest
import numpy as np

def divide(a, b):
    return a / b

def test_pytest_approx():
    result = divide(1, 3)
    assert result == pytest.approx(0.3333333333333333)


def test_assert_approx_equal():
    result = divide(1, 3)
    np.testing.assert_approx_equal(result, 0.3333333333333333, significant=6)

This code comprises two test functions that verify the behavior of the divide function using different approaches for approximate comparisons.

pytest-approx

The first test uses the Pytest framework’s built-in pytest.approx function, while the second test utilizes NumPy’s assert_approx_equal function to achieve the same outcome.

In summary, if you are using Pytest and prefer a more concise syntax and integration with Pytest’s reporting, pytest.approx is a good choice.

However, if you have specific numerical requirements, need fine-tuned control over tolerances, or are working heavily with NumPy, then np.testing.assert_approx_equal is a powerful alternative.

Pytest Approx vs. Numpy’s `assert_allclose`

While both Pytest Approx and Numpy’s assert_allclose serve similar purposes, they differ in syntax and ecosystem integration.

The arguments for Numpy’s assert_allclose are the value you want to test, the expected value, and ‘rtol’, which specifies the relative tolerance.

Please check out our section on Relative Tolerance above to understand relative tolerance better.

Numpy’s function is more focused on NumPy arrays and offers additional options, while Pytest Approx provides a unified approach for all data types and integrates seamlessly with the Pytest framework.

We will look at a sample code to highlight the difference in syntax of both these methods:

tests/unit/test_pytest_approx_5.py

import pytest
import numpy as np

# A function that calculates the square root of a number
def calculate_square_root(x):
    return np.sqrt(x)

def test_pytest_approx():
    result = calculate_square_root(2)
    expected_result = 1.41421356
    assert result == pytest.approx(expected_result, rel=1e-5)

def test_numpy_assert_allclose():
    result = calculate_square_root(2)
    expected_result = 1.41421356
    np.testing.assert_allclose(result, expected_result, rtol=1e-5)

The above code, as you can see, consists of two test functions that assess the behavior of the calculate_square_root function using different techniques for approximate comparisons.

If you are working primarily with NumPy arrays and functions or require advanced options for tolerance control, assert_allclose is a good choice.

pytest-approx

You will notice that both these methods produce the same result and the test cases will pass.

Limitations of Pytest Approx

While Pytest Approx is powerful, it’s important to be aware of its limitations.

It might not be suitable for all scenarios, especially when dealing with extremely small or large numbers where relative tolerances can become impractical.

It’s also not designed for comparisons involving non-numeric data types.

So what should you do when pytest approx doesn’t give you the desired result?

Well, if dealing with extremely small or large numbers, consider using custom comparison functions that directly check for equality or approximate equality based on a fixed threshold.

Or when working with large matrices, Numpy functions like assert_allclose and assert_array_almost_equal may just be the better choice.

Conclusion and Learnings

Having read this article, I’m sure you’re intrigued to try Pytest approx in your own work. It helps you validate floating-point calculations without being hindered by minute numerical differences, thus preventing unnecessary test failures.

In this article, you learnt how pytest approx allows you to specify acceptable tolerances for comparing numerical values using concepts like absolute and relative tolerance.

Whether you’re comparing simple or complex data types, pytest approx helps ensure consistent results.

We also covered how pytest-approx is a better and more efficient method than some more tedious counterpart techniques.

Lastly, we discussed the shortcomings of pytest approx and how exact high precision floating point approximation can be hard to achieve with very large numbers.

Conclusively, by understanding and applying the various strategies offered by Pytest Approx, you can bolster the effectiveness of your tests, ultimately contributing to the stability and quality of your software projects.

If you have any ideas for improvement or like me to cover any topics please comment below or send me a message via Twitter, GitHub or Email.

Till the next time… Cheers!

Additional Reading

https://docs.pytest.org/en/7.1.x/reference/reference.html#pytest-approx
https://happytest-apidoc.readthedocs.io/en/latest/api/pytest/

Importance of Approximations in Testing

The Issue With Floating Point Arithmetic

Solve Numeric Approximation Problems Using Pytest Approx

Objectives

Prerequisites

Set-up and Installations

Understanding Tolerance Levels

Basic Use of Pytest Approx

Syntax of Pytest Approx

Example Code To Test Pytest Approx

Assert Floating-Point Numbers Are Equal - The Issue

Different Approaches to Approximation

Absolute Tolerance:

Relative Tolerance:

Scaling Factors:

Handling NaN values:

Using Custom Comparators:

Handling Complex Data Structures With Pytest Approx

Approximating Lists And Arrays

Approximating Dictionaries

Pytest Approx vs. Numpy’s assert_approx_equal

Pytest Approx vs. Numpy’s assert_allclose

Limitations of Pytest Approx

Conclusion and Learnings

Additional Reading

Pytest Approx vs. Numpy’s `assert_approx_equal`

Pytest Approx vs. Numpy’s `assert_allclose`